Висота трикутника: прості способи обчислення та побудови
Коли ми вперше знайомимось з геометрією в школі, трикутник стає для нас першою фігурою, яка відкриває двері в світ точних побудов і розрахунків. Висота трикутника — одне з тих понять, які здаються простими, але містять глибокий зміст і практичну користь.
Що таке висота трикутника
Висота трикутника — це відрізок, проведений з вершини трикутника до протилежної сторони (або її продовження) під прямим кутом. Кожен трикутник має три висоти — по одній з кожної вершини.
Основа висоти — це точка, в якій висота перетинає протилежну сторону або її продовження. Довжина висоти — це відстань від вершини до основи висоти.
Коли ми розглядаємо висоту, ми говоримо про перпендикуляр, тобто лінію, яка утворює з основою кут 90 градусів.
Як висоти розташовані в різних трикутниках
Положення висот залежить від виду трикутника:
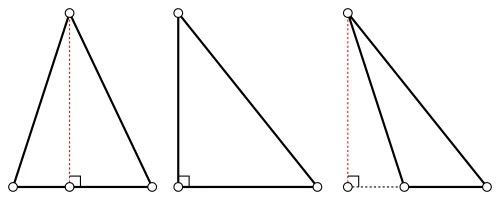
- У гострокутному трикутнику всі висоти проходять всередині фігури. Це схоже на те, як промені світла, спрямовані з кожної вершини, падають всередину трикутника.
- У прямокутному трикутнику дві висоти збігаються з катетами. Третя висота — це перпендикуляр, опущений з вершини прямого кута на гіпотенузу. Ви можете уявити це як драбину, приставлену до стіни, де висота — це сама драбина.
- У тупокутному трикутнику дві висоти лежать поза межами трикутника. Лише висота з тупого кута проходить всередині фігури. Це нагадує тінь, яка виходить за межі предмета при певному освітленні.
 Ортоцентр — місце зустрічі висот
Ортоцентр — місце зустрічі висот
Ортоцентр — це точка перетину всіх трьох висот трикутника. Ця точка має цікаві властивості:
- У гострокутному трикутнику ортоцентр лежить всередині трикутника.
- У прямокутному трикутнику ортоцентр збігається з вершиною прямого кута.
- У тупокутному трикутнику ортоцентр лежить поза межами трикутника.
Ортоцентр входить до знаменитої лінії Ейлера, яка поєднує його з центроїдом (точкою перетину медіан) та центром описаного кола.
Формули для обчислення висоти
Існує кілька способів знайти висоту трикутника:
- Через площу та основу: h = (2 × S) / a, де S — площа трикутника, a — сторона, до якої проведена висота.
- Для рівностороннього трикутника: h = (√3 / 2) × a, де a — сторона трикутника.
- Для прямокутного трикутника: Висота до гіпотенузи: h = (a × b) / c, де a і b — катети, c — гіпотенуза.
Коли ми використовуємо ці формули, ми можемо швидко обчислити висоту без складних побудов.
 Як побудувати висоту трикутника
Як побудувати висоту трикутника
Для побудови висоти з точки C до сторони AB потрібно:
- Поставити ніжку циркуля в точку C і накреслити дугу радіусом, більшим за приблизну відстань до сторони AB.
- Поставити ніжку циркуля в точки A і B та накреслити дуги, які перетнуть першу дугу.
- З’єднати точку C з точкою перетину дуг.
Ця побудова дає нам точну висоту, яка перпендикулярна до сторони AB.
Приклади задач
Задача 1: Знайти висоту трикутника, якщо його площа 24 см², а сторона, до якої проведена висота, дорівнює 8 см.
Розв’язання: h = (2 × S) / a = (2 × 24) / 8 = 48 / 8 = 6 см
Задача 2: У рівносторонньому трикутнику зі стороною 10 см знайти висоту.
Розв’язання: h = (√3 / 2) × a = (√3 / 2) × 10 ≈ 8,66 см
Висота трикутника — це не просто лінія, а потужний інструмент для розв’язання геометричних задач. Знання формул та властивостей висот допоможе вам розв’язувати задачі з геометрії та краще зрозуміти структуру трикутників.
Вивчайте властивості висот разом з медіанами та бісектрисами, і ви побачите, як геометрія розкриває свої таємниці через ці прості, але важливі елементи.

 Ортоцентр — місце зустрічі висот
Ортоцентр — місце зустрічі висот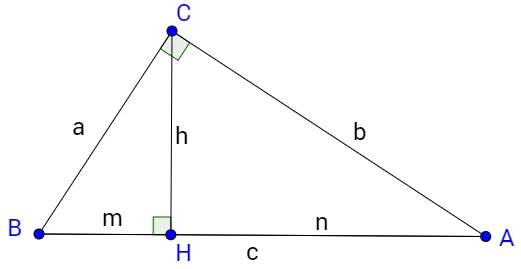 Як побудувати висоту трикутника
Як побудувати висоту трикутника